
A Fractional Diffusion Model for Dye-Sensitized Solar Cells
Dye-sensitized solar cells have continued to receive much attention since their introduction by O‘Regan and Grätzel in 1991. Modelling charge transfer during the sensitization process is one of several active research areas for the development of dye-sensitized solar cells in order to control and improve their performance and efficiency. Mathematical models for transport of electron density inside nanoporous semiconductors based on diffusion equations have been shown to give good agreement with results observed experimentally. However, the process of charge transfer in dye-sensitized solar cells is complicated and many issues are in need of further investigation, such as the effect of the porous structure of the semiconductor and the recombination of electrons at the interfaces between the semiconductor and electrolyte couple. This paper proposes a new model for electron transport inside the conduction band of a dye-sensitized solar cell comprising of TiO2 as its nanoporous semiconductor. This model is based on fractional diffusion equations, taking into consideration the random walk network of TiO2. Finally, the paper presents numerical solutions of the fractional diffusion model to demonstrate the effect of the fractal geometry of TiO2 on the fundamental performance parameters of dye-sensitized solar cells, such as the short-circuit current density, open-circuit voltage and efficiency.

Radiation and inclined magnetic field effects on Williamson fluid flow above a stretching sheet in the existence of velocity, thermal, and concentration slips
Research has been conducted on the study of the multi-slip impact on the Williamson fluid flow above a stretching sheet in the existence of an inclined magnetic field and Radiation. By applying the proper similarity conversions, the governing equations (PDEs) are reduced to a set of non-linear ODEs, and a numerical solution is produced by using MATLAB in-built solver bvp4c package. The impacts of the dimensionless characteristics on the flow patterns are analyzed visually, and the values of the friction, Nusselt, and mass transfer quantities are tabulated to exemplify how the various physical factors have an influence. As the magnetic parameter strength increases, the fluid velocity decreases, but it increases with mixed convection. As the parameters of Brownian motion and thermophoresis increase, the temperature also increases. The findings provide good agreement when compared to the current literature.
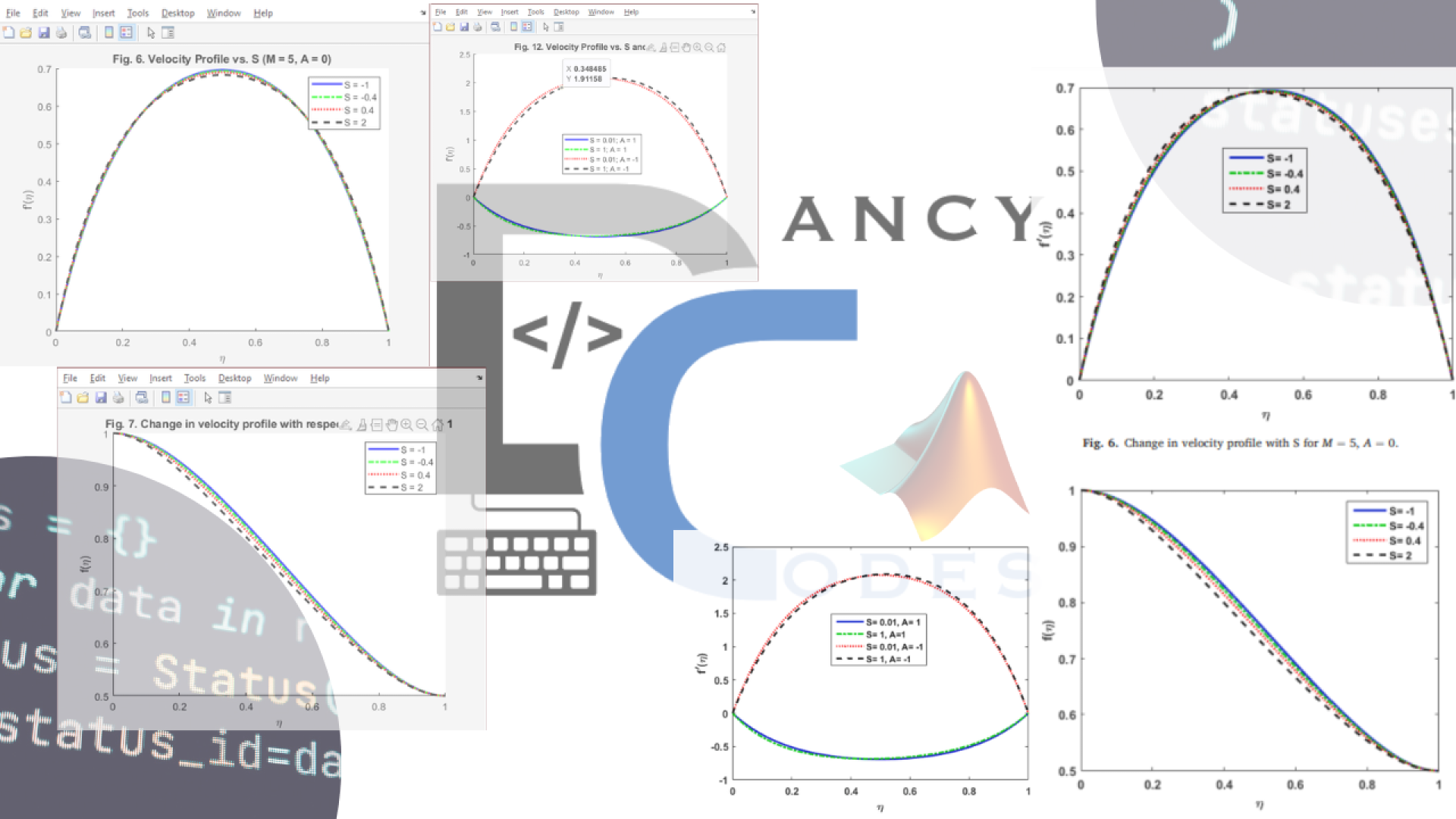
Numerical treatment of squeezed fluid flow under the magnetic influence amid parallel disks
Detailed investigation has been carried out to examine the behavior of squeezed fluid flow under the magnetic influence amid two infinitely extended disks arranged parallel to each other. Porosity is introduced in the lower disk to study the fluid flow characteristics. Applications in engineering and industrial processes, such as cooling systems and chemical reactors, where magnetic fields regulate fluid flow, need a thorough understanding of this phenomenon. The funamdental equations of Navier Stokes (N-S) Equations in the form of Partial Differential Equations (PDEs) are transformed into Ordinary Differential Equations (ODEs) with the help of similarity tranformation. For ensuring better accuracy MATLABs powerful tool is employed in the form of BVP4C technique, to compute the numerical solution. Fluid flow characteristics are discussed for the stated geometry. The velocity profile is discussed under variations of Non-dimensional parameters (Hartman Ha, Squeezed S, suction / injection A). Major findings of the current research revealed that the effect of the Hartmann Number on greatest value of velocity profile is more remarkable in the case of injection compared to suction. Moreover, Velocity profile exhibits a consistent increase as η rises in both scenarios without injection (A = 0) and with injection (A < 0). Current study opens new avenues in terms of exploration of fluid flow characteristics in context of simplicity, accuracy and verstality of numerical techniques.

Effects of thermophoresis and Brownian motion for thermal and chemically reacting Casson nanofluid flow over a linearly stretching sheet
The current research explores the problem of steady laminar flow of nanofluid on a two dimensional boundary layer using heat transfer of Cassona cross the linearly stretching sheet. The governing equations are partial differential equations which are transformed into non-linear ordinary differential equations by using some similarity transformation. The converted form of the combined non-linear higher-order ODEswith a set of boundary conditions are solved by means of Runge-Kutta 4th-order approach along with the shooting method. The nanoparticle concentration profiles, velocity, and temperature are examined by taking account of their influence of Prandtl number, “Brownian motion parameter”, Lewis number, thermophoresis, and Casson fluid parameter. It is reported that the temperature increase as Nt and Nb increases which causes thickening of the thermal boundary layer. Also it is observed that, there is increment in temperature profile for increasing values of Brownian motion parameter and the energy distribution grows with increment in the values of Thermophoresis parameter. The comparison for the local Nusselt & local Sherwood number has been tabulated with respect to variation of the Brownian Motion Parameter and Thermophoresis parameter. All the findings of the results are graphically represented and discussed.

MATLAB Code Package for Solving BVPs with the Shooting and Runge-Kutta Methods
A versatile code package that can be applied to a wide range of BVPs, including non-linear problems, making it perfect for researchers, engineers, and students alike. The BVP Shoot Solver Package uses the shooting method with the Runge-Kutta 4th order numerical integration technique, ensuring reliable and precise results.